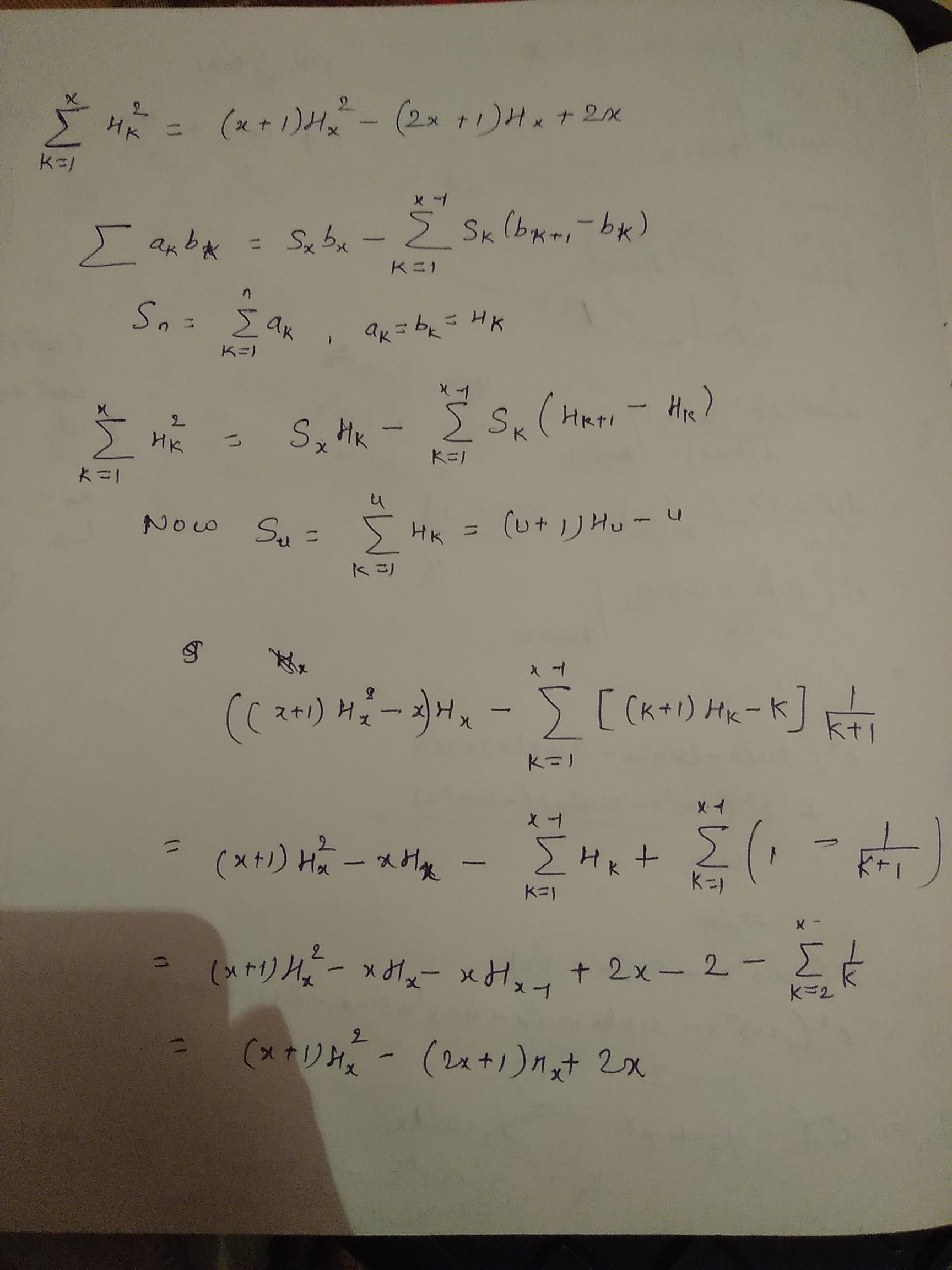Question

Let $H_n$ be the $n^{th}$ harmonic number, $$ H_n = \sum_{i=1}^{n} \frac{1}{i} $$ Question: Calculate the following $$\sum_{j=1}^{n} H_j^2.$$ I have attempted a generating function approach but could not solve this.

Answer

$$\sum_{k =1}^xH_k^2 = (x+1)H_x^2 - (2x+1)H_x + 2x$$

Before we prove the above solution consider this following $$\begin{align*} \color{blue}{\sum_{k =1}^{x}H_k} &=\sum_{k =1}^{x}\sum_{n =1}^{k}\frac 1{n}=\sum_{k =1}^{x}\frac 1{n}\sum_{k =n}^{x}1 = \sum_{k =1}^{x}\frac 1{n}(x-n+1)\\ &=\sum_{k =1}^{x}\frac {(x+1)-n}{n} =(x+1)\sum_{k =1}^{x}\frac 1{n} - \sum_{k =1}^{x}1 = \color{blue}{(x+1)H_x - x = \sum_{k =1}^{x}H_k} \end{align*}$$

Consider, $$\sum_{k =1}^xa_kb_k = s_xb_x- \sum_{k = 1}^{x-1}s_k(b_{k+1}-b_k)\text{ Where } s_u =\sum_{k =1}^ua_k$$

Put: $a_k = b_k = H_k$

$$\begin{align*} \color{blue}{\sum_{k =1}^xH^2_k} & = s_xH_k- \sum_{k =1}^{x-1}s_k(H_{k+1}- H_k)\\ & =((x+1)H_x-x)H_k -\sum_{k =1}^{x-1}[(k+1)H_k - k](\frac 1{k+1})\\ & = (x+1)H^2_x - xH_x - \sum_{k =1}^{x-1}H_k + \sum_{k =1}^{x-1}\left(1-\frac {1}{k+1}\right)\\ & = (x+1)H^2_x-xH_x -xH_{x-1} + 2x - 2- \sum_{k =2}^{x}\frac 1{k}\\ & = \color{blue}{(x+1)H^2_x-(2x+1)H_x +2x} \end{align*}$$