Solving an Integral

Question

Well! I was going through harmonic series from mathworld.worlfram I found harmonic numbers are really tough to calculate I was scribbling and wrote this thing $$\sum_{k = 1}^{x}H_k= \sum_{k =1}^{x}\left(\sum_{u = 1}^{k}\frac 1{u}\right)$$ How can I simplify these highly complicated things Howe can we find this thing At the first, we can't find $H_k$ itself and series over series making it a little hard I wonder how can we simplify this thing? It's just my curiosity....

Answer

Well! then I liked this curiosity I guess by solving you mean just to find only one harmonic number(say: $H_p)$ and finding the above $\sum\sum\frac 1{k}$ This is possible and I solved that by finding a pattern that only the last terms of each harmonic number are making previously calculated harmonic numbers different with only $\frac 1{k-1}$ But for the sake proof of my simplified result, I can provide an easy way $$\begin{align*} S &=\sum_{k =1}^{x}H_k\\ &=\sum_{k =1}^{x}\sum_{n =1}^{k}\frac 1{n}\\ &=\sum_{k =1}^{x}\frac 1{n}\sum_{k =n}^{x}1\\ & = \sum_{k =1}^{x}\frac 1{n}(x-n+1)\\ & =\sum_{k =1}^{x}\frac {(x+1)-n}{n}\\ & =(x+1)\sum_{k =1}^{x}\frac 1{n} - \sum_{k =1}^{x}1\\ & = (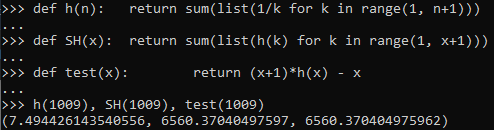x+1)H_x - x \end{align*}$$ Here, SH() & test() is our result expected which are equal.